Posts

Breadth-First Binary Numbers and Their Application to Musical Rhythms

-
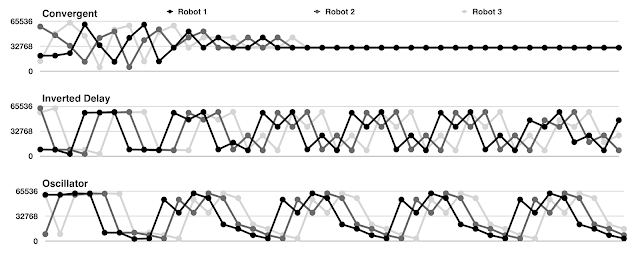
Image
Figure 1. Rhythms encoded by breadth-first binary numbers. Introduction I built some robots recently that play musical rhythms. They are depicted in Figure 2. Figure 2. Dr. Squiggles rhythmic robots, which motivated this rabbit hole. The rhythms in question are all a certain constant number of beats in duration, with a certain constant number of subdivisions per beat. Each subdivision can be populated by an onset or not. For simplicity, say there are always 4 beats and 4 subdivisions per beat (16 subdivision per rhythm). I want to know how the rhythms evolve over time; sometimes a robot might play the same thing over and over, and sometimes it might play something very different every 4 beats. I would like to encode each 16-bit rhythm as an integer, so I can plot the rhythms that each robot plays over time. The obvious thing would be to convert the rhythms directly to integers via binary. The problem is that similar rhythms might not have nearby integers, and vice verc...
Post a Comment
Read more

A note on the strength of note onset strength

-
Image
A note on the strength of note onset strength and the mystical transformative healing power of number theory When we invent algorithms that write music, our research often focuses on pitch, rhythm, timbre, melody, harmony. Note-strength [ 1 ] is typically not the direct focus of research, and is thus often neglected. However, any rendition of music that does not vary note-strength will be tiresome. Here we present a quirk of number theory that can be used as a quick and dirty way to apply a default strength to each note as a post-processing step, for music where the beat locations are known. Let us assume that the notes that are on the beat should be the strongest; those that fall on the half-beat should be the next-strongest, and on the second and fourth quarter beat to be somewhat weaker than that, etc… Assuming the beat occupies times 0 &leq; t < 1, this implies that the strength is inversely proportional to the denominator of the rational representation [ 2 ] of the...
Post a Comment
Read more

How I calibrated my contact microphone

-
Image
Introduction I used the Hsu-Nielson method to find the frequency response of my contact microphones. This method involves cracking a mechanical pencil graphite on the microphone transducer. The microphone in question is the one shown above, and described in detail here: http://michaelkrzyzaniak.com/marshmallow.php I specifically used the white, low-gain variant. Experimental Setup and Results Figure 1: The mechanical pencil used in this experiment, with 0.5mm number-2 graphite Figure 2: Three millimeters of graphite were extended from the pencil Figure 3: Audio interface used for experiment (Scarlett 2i4), showing the settings used. Figure 4: Video showing the graphite being cracked. A small amount of putty was used to prevent the tip of the pencil tapping the transducer after the graphite breaks. The graphite is placed on the transducer and constant pressure is applied. When the graphite breaks, the pressure is released in a very short ti...
Post a Comment
Read more

Take this and put it over there

-
Image
Introduction As part of the Audio Augmented Reality project, we did a pair of workshops as a way of discovering avenues for technologies that people might be interested in. After reviewing the transcripts and having some general discussions with the other team members, I decided to start making a gestural system for placing sounds in 3d space. Implementation The system is to difficult to explain, so I made a quick video. Future Work I'm going to do some of the things I said in the video. And I am going to work on some other prototypes of different systems.
Post a Comment
Read more

Ambisonic Rendering in the Story Bubble

-
Image
Figure 1: Sound Sphere in the Center for Vision, Speech and Signal Processing (CVSSP) at the University of Surrey. The person is shown standing in the intended orientation, facing the front of the sphere. Introduction I recently needed some audio content that I could quickly render for playback in the sound sphere shewn in Figure 1. There are a reasonable amount of free ambisonic recordings available online, e.g. Angelo Farina Youtube So I spent some time putting together tools to render ambisonics in the sphere, and here I wanted to share what I learned in case anybody else at CVSSP wants to try this out in the future. Speaker Arrangement The sphere has 24 speakers (plus a subwoofer which I will henceforth ignore), which at the time of writing are arranged as shown in Figure 2 and Figure 3. Figure 2: Speaker layout. The center of the diagram represents the top of the sphere. The top of the diagram represents the front of the sphere. Th...
Post a Comment
Read more

These 5 definitions of audio augmented reality will blow your mind!

-
Image
A taxonomy of audio augmented reality with examples. Introduction With the new year, I am working on a new project involving audio augmented reality (AAR). I started doing a literature review on the topic, and it turns out that I'm not even sure what the term "audio augmented reality" means. So I started grouping the projects I have seen, and I have identified at least 5 distinct situations that have been or could be, in my estimation, called AAR. These are as follows (with examples): Enchanting silent physical objects with digital sound Enchanted textiles Enchanted paper / books / maps Enchanted footballs / sports equipment Overlay of extra audio information onto the real world sat nav self-guided in-ear museum tours Digital sound-objects placed in real 3d space Sound attached to virtual objects in AR Games Geolocated narrative Geolocated music playlists ...
Post a Comment
Read more

Digital Textiles

-
Image
Introduction Anyone within earshot knows, and is already sick of the fact, that I have been obsessed with knitting and crochet for the past few months. I bought a knitting machine and have been knitting everything from scarves to topological manifolds to non-euclidian surfaces. I've been looking at knit art-installations, Daina Taimina, amigurumi, the hyperbolic crochet coral reef project, and yarn bombing. I convinced myself that knit fabric cannot exist in any dimension other than 3 and that knit fabric, despite the etymology, is topologically not a knot. I re-read Alan-Turing's seminal paper on the Entscheidungsproblem to try to determine if knitting is Turing-complete (I'm still not sure). And I have been trying to design an anti-knitting machine that can annihilate with a knitting machine. Figure 1: Some random things I knit (including a Klein bottle on the right). Conductive Yarn And then I discovered conductive yarn, and it blew my mind. Conductive yarn is mos...
2 comments
Read more