Breadth-First Binary Numbers and Their Application to Musical Rhythms
Figure 1. Rhythms encoded by breadth-first binary numbers.
Introduction
I built some robots recently that play musical rhythms. They are depicted in Figure 2.Figure 2. Dr. Squiggles rhythmic robots, which motivated this rabbit hole.
The rhythms in question are all a certain constant number of beats in duration, with a certain constant number of subdivisions per beat. Each subdivision can be populated by an onset or not. For simplicity, say there are always 4 beats and 4 subdivisions per beat (16 subdivision per rhythm). I want to know how the rhythms evolve over time; sometimes a robot might play the same thing over and over, and sometimes it might play something very different every 4 beats. I would like to encode each 16-bit rhythm as an integer, so I can plot the rhythms that each robot plays over time. The obvious thing would be to convert the rhythms directly to integers via binary. The problem is that similar rhythms might not have nearby integers, and vice verca. For example the integer binary 1000000000000000 (32768 in decimal) is is only one away from binary 0111111111111111 (32767 in decimal), but as rhythms they are very dissimilar. Assuming 1 means the corresponding subdivision is populated by an onset, the first is a very sparse rhythm, and the second is very dense. The rhythms are complements of eachother, they are separated by a large Hamming distance. This issue comes up in a number of circumstances, and there are other binary encodings, such as the Gray Code, that deal with it in particular ways. In my case, I need a code that gives similar rhythms similar integers, assigns nearby integers to rhythms with similar Hamming weights, and makes complementary rhythms easy to indentify.
Breadth-First Binary Encodings
In binary, we typically count in what I will call depth-first order, exhausting every possibility for each rightmost bit before moving one bit to the left. Given a fixed bit-width, I want to count in what I call breadth-first order, exhausting all of the bit positions before setting another bit. For example, for 4-bit numbers:- 0000 == 0
- 0001 == 1
- 0010 == 2
- 0100 == 3
- 1000 == 4
- 0011 == 5
- 0101 == 6
- 1001 == 7
- 0110 == 8
- 1010 == 9
- 1100 == 10
- 0111 == 11
- 1011 == 12
- 1101 == 13
- 1110 == 14
- 1111 == 15
Application to Rhythms
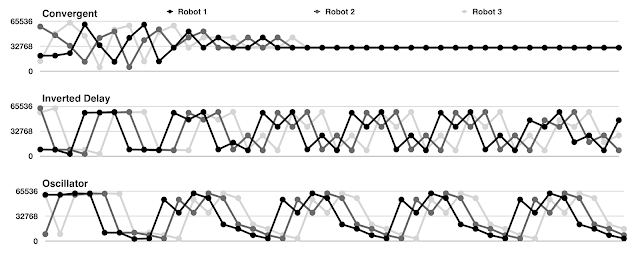
This allows me to plot rhythms over time. Figure 1 shows the rhythms played by three robots listening to eachother in a loop. In the top graph, the three robots play some random rhythms before eventually converging to a single rhythm. In the middle graph, The first robot repeats a cycle of 6 rhythms; 3 random rhythms followed by their complements; while the other two robots play delayed compies of the first robot. In the bottom graph, the first robot plays a cycle of 8 rhythms oscillating between sparse and dense, and again the other two robots play delayed copies of the first. There are a few transcription errors where a robot heard incorrectly and played something slightly different than it should have.OEIS
One problem is that this, at least naively, has intractably high time-complexity for large bit-widths, and due to my feeble mathematical skills, I was unable to find closed form expressions that do the same as the recursive algorithm. In particular, it seems like there should be a known integer sequence a_k(n) in which the nth term is the depth-first decimal representation of the breadth-first binary representation of n, for bit width k. Or the inverse of this. For example,- n bin a_4(n)
- 0 0000 0
- 1 0001 1
- 2 0010 2
- 3 0100 4
- 4 1000 8
- 5 0011 3
- 6 0101 5
- 7 1001 9
- 8 0110 6
- 9 1010 10
- 10 1100 12
- 11 0111 7
- 12 1011 11
- 13 1101 13
- 14 1110 14
- 15 1111 15
Appendix 1 — Recursive Algorithm
#include <stdio.h> #define BOOL int #define NO 0 #define YES (!NO) /*----------------------------------------------------*/ //this is the recursive bit that does all the work BOOL __private_breadth_first_counter(unsigned* counter, int* bits, int bits_width, int num_set_bits, int return_when) { BOOL result = NO; if(*counter == 0) return YES; if(return_when < 0) return_when = 0; if(num_set_bits <= return_when) return NO; if(__private_breadth_first_counter(counter, bits, bits_width, num_set_bits-1, return_when)) return YES; int i; for(i=0; i<bits_width-num_set_bits+1; i++) { bits[i] = 1; if(num_set_bits == 1) --*counter; if(__private_breadth_first_counter(counter, bits+1+i, bits_width-(i+1), num_set_bits-1, num_set_bits-2)) return YES; bits[i] = 0; } return NO; } /*----------------------------------------------------*/ void decimal_to_breadth_first_bits_array(unsigned decimal, int* returned_bits, int bits_width) { int i; for(i=0; i<bits_width; returned_bits[i++] = 0); __private_breadth_first_counter(&decimal, returned_bits, bits_width, bits_width, 0); } /*----------------------------------------------------*/ unsigned decimal_to_breadth_first_bits_int(unsigned decimal, int bits_width) { int i; unsigned result = 0; int bits_array[bits_width]; decimal_to_breadth_first_bits_array(decimal, bits_array, bits_width); for(i=0; i<bits_width; i++) result |= bits_array[i] << i; return result; } /*----------------------------------------------------*/ int main() { const int width = 4; int max = 1 << width; int i; for(i=0; i<max; i++) { unsigned bits_int = decimal_to_breadth_first_bits_int(i, width); printf("%i\t%i\r\n", bits_int, i); } }



Comments
Post a Comment